1種冷凍学識計算攻略-問1：熱収支攻略
EchoLand-plus
さぁ、熱収支を攻略しよう！
多段圧縮機の問題を解きながら、熱収支を攻略していきましょう。
第一種冷凍機械責任者学識試験 平成18年度 問1
問1 R22を冷媒とする二段圧縮二段膨張冷凍装置の概略図および理論冷凍サイクルは、下図の通りである。この装置について、 次の(1)、(2)、(3)および(4)の問に、解答用紙の所定欄に計算式を示して答えよ。
ただし、低段側の冷媒循環量はqmro ＝ 0.2kg/sであり、この理論冷凍サイクルの各状態点における比エンタルピーの値は、下記の通りである。（20点）
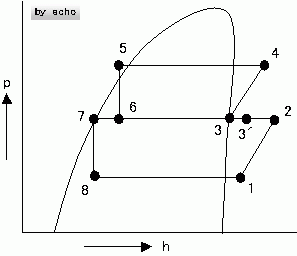
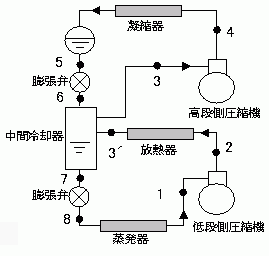
（運転条件）
h1 ＝ 400kJ/kg
h2 ＝ 440kJ/kg
h3´ ＝ 420kJ/kg
h3 ＝ 405kJ/kg
h4 ＝ 435kJ/kg
h5 ＝ h6 ＝ 230kJ/kg
h7 ＝ h8 ＝ 200kJ/kg
（1）冷凍能力Φo（kW）を求めよ。
（2）高段側の冷媒循環量qmrk（kg/s）を求めよ。
（3）圧縮機の総理論圧縮軸動力Pth（ｋW）を求めよ。
（4）理論成績係数（COP)thを求めよ。
（1）冷凍能力Φo（kW）を求めよ
軽くこなします。基本式はこれ、
Φo ＝ qmro（h1 － h8）
答え Φo ＝ 40（kW）
（2）高段側の冷媒循環量qmrk（kg/s）を求めよ。
この問題では、中間冷却の熱収支を考えます。これができないと、（1）しか得点できないでしょう。
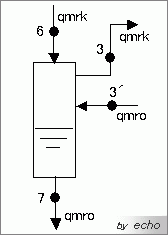
図を見てください、中間冷却器部分を抜き出して書いてみました。
ここで、左辺に入るもの、右辺に出るものを書きます。（青と赤に色を変えてみます。）
放熱器があって惑わされます？が、関係ないので無視します。
えぃ、！！
qmrk・h6 ＋ qmro・h3´ ＝ qmrk・h3 ＋ qmro・h7
これまでできれば、qmroは問題文で指定されていますから、もう解けたも同然ですよ！
qmroとqmrkをまとめます（大きい比エンタルピーから小さい方を引き算するように）
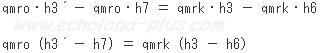
よって、
答え qmrk ＝ 0.251（kg/s）
と、まぁ、中間冷却器の熱収支さえ導き出す事ができれば簡単なのです。
（3） 圧縮機の総理論圧縮軸動力Pth（ｋW）を求めよ。
理論ですし、ルンルン気分で解きます。
低段側と高段側の理論圧縮軸動力の和！ですね！・・・何も考えずに解きます。（h3´に惑わされないように）
答え Pth ＝ 15.53（kW）
（4）理論成績係数（COP)thを求めよ。
怒濤のごとく一気に片付けます！
（1）と（3）で、求めた冷凍能力Φoと理論圧縮軸動力Pthを使います。（問題の主旨もそうなっているかと思います）
答え (COP)th ＝ 2.58
どうでしょう、中間冷却器の熱収支さえ分かれば、あとは二種冷凍の学識で得た知識で十分こと足ります。 次は、検定講習試験で出題された問題を攻略してみましょう。
第一種冷凍学識試験【講習検定】 平成18年度 問1
講習検定試験の問題は「二段圧縮一段膨張冷凍装置」です。図や線図がありません文字だけです。
イメージとして装置の様子が浮かびそのまま式を立てることが出来れば良いですが・・・。ま、図と線図をサクサクと書けるようになりましょう！
さっそく、概略図とp-h線図を書いてみましょう。
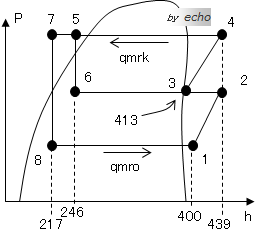
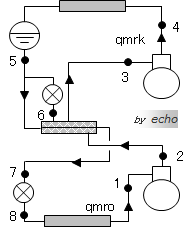
こんな感じですね。
（1）凝縮負荷Φk（kW）を求めよ。
サクッと？片付けます！
問題には、水冷凝縮器の冷却水量qmw、冷却水のΔt、比熱cwが指定されていますから、下の式を使います。この式の説明はとくにしません、テキストを読んでいれば 大丈夫だと思います。この後、熱の問題で嫌になるほど出てきますし…。
Φk ＝ cw・qmw・Δt ＝ 4.2 × 10 × 5 ＝ 210（kW）
答え Φk ＝ 210（kW）
（2）冷凍能力Φo（kW）を求めよ。
これも熱収支が一番のカギ。
冷凍能力Φoは、
Φo ＝ qmro（h1 － h8）…（1）
ここで、h7 ＝ h8であるから、この（1）式の中でqmroが分かればΦoを求められます。
さて、頭をひねります・・・。はい、そうです、そうです。中間冷却器の熱収支にはqmroが含まれているはずです。
とにかく、熱収支の式を書いてみます。ぉっと、その前に中間冷却器部分を抜き出して図に書いてみましょう。
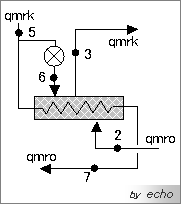
如何ですか、サクッとかけましたか。
では、
入るものを左辺、出るものを右辺に並べてみます。
ぇぃ。
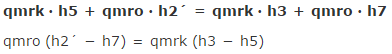
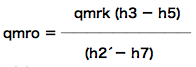…（2）
これで、qmroが求められそうですが、qmrkが分かりません。 それと、h2´ですね。
このあたりは、2種冷凍で勉強しました。分からない方は、上級テキストの55ページあたり、 または、2種冷凍学識攻略「「機械的損失仕事は冷媒に熱として加わらないものとする」とは？」ページを見てください。（別窓で開きます）
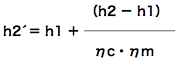…（3）
数値代入して、
では、サクッと？qmrkを求めます。そうです、問（1）で求めた凝縮負荷Φkを使います。
Φk ＝ qmrk (h4´－ h5) …（4）
ここで注意するのは、低段側のh2´同様、高段側でもh4´です！
まずは、h4´を求めます。
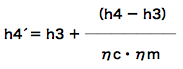…（5）
数値代入して、
h4´を求めたので、（4）式からqmrkを求めます。
よって、qmroは（2）式を用いて、
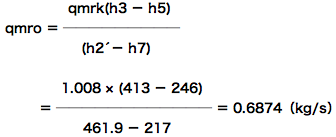
やっとここまで来ました・・・（1）式に、qmroを代入しΦoを求めます！
Φo ＝ qmro (h1 － h8) ここに、h7 ＝ h8（←まごつかないように、p-h線図を見れば分かります。）
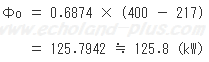
答え Φo ＝ 125.8（kW）
（3） 圧縮機所要動力P（kW）を求めよ。
動力Pを求めるには…。そうです、そうです、そのとおり。せっかく、（1）と（2）で凝縮負荷Φkと冷凍能力Φoを求めたのですからねぇ。
Φk ＝ Φo ＋ P …（6）
この式は、基本中の基本ですが二種冷凍ではあまり出てきませんでした。一種になるとヒョッコリ顔を出したりします。
（6）式よりPは、
低段側動力PLと高段側動力PHの和でも求められます。試験時間に余裕があったら確かめてみましょう。
答え P ＝ 84.2（kW）
めでたしめでたし...それにしても、長々とかかってしまいました。このように長くなると、書くところが無くなってしまうかも知れません。チョとまとめておきましょう。
こんな感じでどうでしょうか、まだチョと長いかもしれませんね。（低段側冷媒循環量qmro、高段側冷媒循環量qmrkとする） みたいな説明は、スペースや時間がなかったら省いても大丈夫だと思います。（・・・・・たぶんね） ちなみに、思い切って省いた解答例を書いてみます。
（1） Φk ＝ cw・qmw・Δt ＝ 4.2 × 10 × 5 ＝ 210 答 210（kW）
（2） Φo ＝ qmro（h1 － h8） ＝ 0.6874 × (400 － 217) ＝ 125.8 答 12 5.8（kW）
（3） P ＝ Φk － Φo ＝ 210 － 125.8 ＝ 84.2 答 84.2（kW）
どうでしょうね・・・20点満点もらえますかね。微妙～？・・・・ま、解答欄が、3行ほどのスペースだったらこれで満点かと思います。 たっぷりスペースがあったけど、時間がなかった～！ってのは、許してもらえないかもしれません。
要は、この出題者が何を問うているのか・・・です。この場合は、熱収支を理解していて、理論値ではなく実際の値で導き出しているか だと、思います。
あと、答えが微妙に違う場合がありますが、許容範囲内あれば良いと思います。（ただし、式が間違っていれば駄目だと思いますよ） 冷媒循環流量は小数点以下3桁まで求めたほうがいいです。
上記のように0.6874みたいに4桁目が微妙～なものは4桁ね。そうするとわりと、 模範解答と同じような答えになります。過去問こなすとこのあたりは分かってくるはず・・・・です。
この解答で満点じゃなかったら、試験官（採点者）がおかしい！！・・・ぐらい、勉強してみましょう。
訂正箇所履歴
【2016/10/22 新設】
- 計算式がスマホなどで崩れるため、自動で大きさが変化する画像にした。解説文等も見直し。（2017/04/01）